Action–Wave Space (AWS) is a unified framework that starts from a single real scalar phase field on a four–dimensional “action–space” geometry. From this single ingredient, spacetime, quantum behaviour, and familiar particles and fields appear only after a causal projection to ordinary spacetime. The aim of the AWS programme is to rebuild quantum theory, gravity, and the Standard Model from this common geometric origin.
On this page you find a conceptual overview of the core idea. More detailed technical material and the full stack of AWS research papers are collected on the Framework page. For a background story in plain, layman’s terms, see the Origins page.
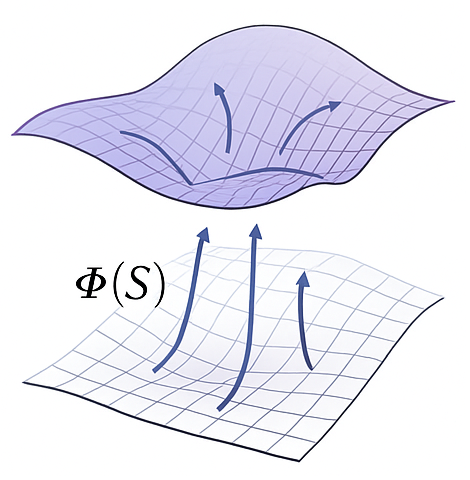
Single real scalar field \(\Phi(S^\mu)\) defined on a four-dimensional Lorentzian symplectic manifold \(\mathscr{M}_{\text{AWS}}\). Its phase gradients \(\partial_\mu \Phi\) generate the metric and symplectic structure, and source curvature dynamically.
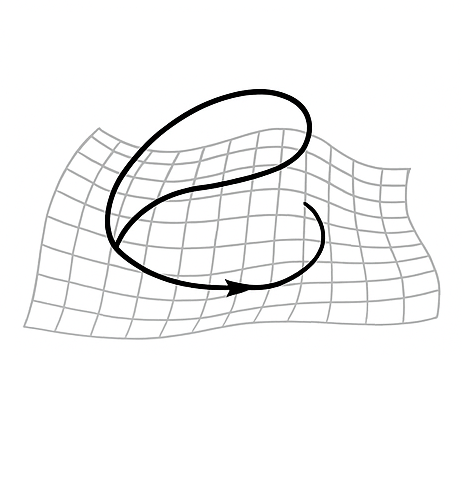
Curvature leads to the formation of scalartons: compact, topologically constrained domains \(D_x = \pi^{-1}(x)\) satisfying \((\chi, b_1, b_2) = (2, 1, 3)\). These domains trap scalar flux and support interference-stable quantization.

Observable particles and fields \(\psi(x)\) in emergent spacetime arise via causal projection \(\pi: \mathscr{M}_{\text{AWS}} \to M_4\) through a scalar-derived kernel \(G_R(x, S)\).
Action–Wave Space (AWS) starts from a single first principle: only Action exists and its flux is conserved. From this assumption one is led to a single real scalar phase field \(\Phi\) on a four–dimensional Lorentzian–symplectic manifold \((M,g,\Omega)\). AWS is obtained by a phase–space compression: starting from the eight–dimensional cotangent bundle \(T^{*}M_{4}\) with coordinates \((x^\mu,p_\mu)\), the Hamilton–Jacobi condition \(p_\mu = \partial_\mu \Phi\) eliminates independent momentum coordinates and defines intrinsic “action–like” labels \(S^\mu\) on a reduced 4D Action–Wave Space. The closed two–form \(\Omega := d(d\Phi)\) encodes quantized Action flux on compact 2–cycles, \(\int_{\Sigma} \Omega = 2\pi n\hbar\), and the AWS field equation together with metric–symplectic compatibility follow from a single covariant, shift–symmetric action for \(\Phi\). Quantization is not postulated but emerges from global phase coherence and flux integrality on \((M,g,\Omega)\).
Observable physics appears only after projection from AWS to effective spacetime. A causal projection map \(\pi : M \to M_4\) associates to each spacetime event \(x^\mu\) a compact preimage (a “scalarton”) \(D_x = \pi^{-1}(x)\) with fixed topology \((\chi,b_1,b_2) = (2,1,3)\). A retarded kernel \(G_R(x,S)\), derived from the AWS dynamics, filters globally coherent phase configurations on \(D_x\) into spacetime amplitudes \(\psi(x) = \int_{D_x} G_R(x,S)\,A(S)\,e^{i\Phi(S)/\hbar}\,\sqrt{-g(S)}\,d^4S\). This compact, quantized fiber structure enforces interference stability and flux quantization, and it is this topology–plus–projection mechanism that underpins the emergence of the spacetime metric, quantum probabilities, gauge fields, spin/statistics, and the observed pattern of fermion generations from a single scalar phase geometry.
